Теорема о высоте прямоугольного треугольника

Если высота в прямоугольном треугольнике ABC длиной , проведённая из вершины прямого угла, делит гипотенузу длиной на отрезки и , соответствующие катетам и , то верны следующие равенства:

·

·

Свойства оснований высот треугольника

· Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.

· Описанная около ортотреугольника окружность - окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.

Другая формулировка последнего свойства:

· Теорема Эйлера для окружности девяти точек .

Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек ).

· Теорема . В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.

· Теорема . В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.

Другие свойства высот треугольника

· Если треугольник разносторонний (неравносторонний ), то его внутренняя биссектриса, проведённая из любой вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.

· Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности , проведенному из той же самой вершины.

· В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

· В прямоугольном треугольнике высота , проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Свойства минимальной из высот треугольника

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

· Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.

· Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.

· При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.

· Минимальная высота в треугольнике всегда проходит внутри этого треугольника.

Основные соотношения

· где - площадь треугольника, - длина стороны треугольника, на которую опущена высота.

· где - произведение боковых сторон, радиус описанной окружности

· ,

где - радиус вписанной окружности.

Где - площадь треугольника.

где - сторона треугольника, к которой опускается высота .

· Высота равнобедренного треугольника, опущенная на основание:

где - основание.

· - высота в равностороннем треугольнике.

Медианы и высоты в равностороннем треугольнике

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. А в равносторонних треугольниках медианы и высоты - одно и то же.

Рассмотрим произвольный треугольник ABC. Обозначим буквой O точку пересечения его медиан AA1 и BB1 и проведем среднюю линию A1B1 этого треугольника Медианы треугольника пересекаются в одной точке Отрезок A1B1 параллелен стороне AB, поэтому углы 1 и 2, а также углы 3 и 4 равны как накрест лежащие углы при пересечении параллельных прямых AB и A1B1 секущими AA1 и BB1. Следовательно, треугольники AOB и A1OB1 подобны по двум углам, и, значит их стороны пропорциональны: AOA1O=BOB1O=ABA1B1 . Но AB=2⋅A1B1, поэтому AO=2⋅A1O и BO=2⋅B1O. Таким образом, точка O пересечения медиан AA1 и BB1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка пересечения медиан BB1 и CC1 делит каждую из них в отношении 2:1 считая от вершины, и, следовательно, совпадает с точкой O. Итак, все три медианы треугольника ABC пересекаются в точке O и делятся ею в отношении 2:1, считая от вершины.

Теорема доказана.

Представим что в вершинах угла m₁=1, тогда в точках A₁,B₁,C₁, m₂=2, так как они являются серединами сторон. И тут можно заметить, что отрезки AA₁,BB₁,CC₁, которые пересекаются в одной точке и похожи на рычаги с точкой опоры О, где AO-l₁, a OA₁-l₂(плечи). И по физической формуле F₁/F₂=l₁/l₂, где F=m*g, где g-const, и она соответственно сокращается, получается m₁/m₂=l₁/l₂ т.е. ½=1/2.

Теорема доказана.

Ортотреугольник

Свойства:

· Три вы­со­ты тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке, эта точка носит на­зва­ние ор­то­цен­тра

· Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника

· Высоты треугольника являются биссектрисами ортотреугольника

· Ортотреугольник-это треугольник с наименьшим периметром, который можно вписать в данный треугольник (задача Фаньяно)

· Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла из которого он исходит.

· Если точки A 1 , B 1 и C 1 на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

то - ортотреугольник треугольника ABC.

Ортотреугольник отсекает треугольники, подобные данному

Теорема о свойстве биссектрис ортотреугольника

∟ B₁C₁C=∟B₁BC=∟CAA₁=∟CC₁A

CC₁-биссектриса ∟B₁C₁A

AA₁-биссектриса ∟B₁A₁C₁

BB₁-биссектриса ∟A₁B₁C₁

Треугольники.

Основные понятия.

Треугольник - это фигура, состоящая из трех отрезков и трех точек, не лежащих на одной прямой.

Отрезки называются сторонами , а точки - вершинами .

Сумма углов треугольника равна 180 º .

Высота треугольника.

Высота треугольника - это перпендикуляр, проведенный из вершины к противолежащей стороне.

В остроугольном треугольнике высота содержится внутри треугольника (рис.1).

В прямоугольном треугольнике катеты являются высотами треугольника (рис.2).

В тупоугольном треугольнике высота проходит вне треугольника (рис.3).

Свойства высоты треугольника:

Биссектриса треугольника.

Биссектриса треугольника - это отрезок, который делит угол вершины пополам и соединяет вершину с точкой на противолежащей стороне (рис.5).

Свойства биссектрисы:

Медиана треугольника.

Медиана треугольника - это отрезок, соединяющий вершину с серединой противолежащей стороны (рис.9а).

Длину медианы можно вычислить по формуле: 2b 2 + 2c 2 - a 2 m a 2 = —————— 4 где m a - медиана, проведенная к стороне а . В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы: c m c = — 2 где m c - медиана, проведенная к гипотенузе c (рис.9в) Медианы треугольника пересекаются в одной точке (в центре масс треугольника) и делятся этой точкой в соотношении 2:1, отсчитывая от вершины. То есть отрезок от вершины к центру в два раза больше отрезка от центра к стороне треугольника (рис.9с). Три медианы треугольника делят его на шесть равновеликих треугольников.

Средняя линия треугольника.

Средняя линия треугольника - это отрезок, соединяющий середины двух его сторон (рис.10).

Средняя линия треугольника параллельна третьей стороне и равна ее половине

Внешний угол треугольника.

Внешний угол треугольника равен сумме двух несмежных внутренних углов (рис.11).

Внешний угол треугольника больше любого несмежного угла.

Прямоугольный треугольник.

Прямоугольный треугольник - это треугольник, у которого есть прямой угол (рис.12).

Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой .

Две другие стороны называются катетами .

Пропорциональные отрезки в прямоугольном треугольнике.

1) В прямоугольном треугольнике высота, проведенная из прямого угла, образует три подобных треугольника: ABC, ACH и HCB (рис.14а). Соответственно, углы, образуемые высотой, равны углам А и В.

Рис.14а

Равнобедренный треугольник.

Равнобедренный треугольник - это треугольник, у которого две стороны равны (рис.13).

Эти равные стороны называются боковыми сторонами , а третья - основанием треугольника.

В равнобедренном треугольнике углы при основании равны. (В нашем треугольнике угол А равен углу C).

В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника.

Равносторонний треугольник.

Равносторонний треугольник - это треугольник, у которого все стороны равны (рис.14).

Свойства равностороннего треугольника:

Замечательные свойства треугольников.

У треугольников есть оригинальные свойства, которые помогут вам успешно решать задачи, связанные с этими фигурами. Некоторые из этих свойств изложены выше. Но повторяем их еще раз, добавив к ним несколько других замечательных особенностей:

1) В прямоугольном треугольнике с углами 90º, 30º и 60º катет b , лежащий напротив угла в 30º, равен половине гипотенузы. А катет a больше катета b в √3 раз (рис.15а ). К примеру, если катет b равен 5, то гипотенуза c обязательно равна 10, а катет а равен 5√3. 2) В прямоугольном равнобедренном треугольнике с углами 90º, 45º и 45º гипотенуза в √2 раз больше катета (рис.15b ). К примеру, если катеты равны 5, то гипотенуза равна 5√2. 3) Средняя линия треугольника равна половине параллельной стороны (рис.15с ). К примеру, если сторона треугольника равна 10, то параллельная ей средняя линия равна 5. 4) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы (рис.9в): m c = с/2. 5) Медианы треугольника, пересекаясь в одной точке, делятся этой точкой в соотношении 2:1. То есть отрезок от вершины к точке пересечения медиан в два раза больше отрезка от точки пересечения медиан к стороне треугольника (рис.9c) 6) В прямоугольном треугольнике середина гипотенузы является центром описанной окружности (рис.15d ).

Признаки равенства треугольников .

Первый признак равенства : если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства : если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства : если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Неравенство треугольника.

В любом треугольнике каждая сторона меньше суммы двух других сторон.

Теорема Пифагора.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

c 2 = a 2 + b 2 .

Площадь треугольника.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

ah
S = ——
2

2) Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними:

1
S = — AB · AC · sin A
2

Треугольник, описанный около окружности.

Окружность называется вписанной в треугольник, если она касается всех его сторон (рис.16а ).

Треугольник, вписанный в окружность.

Треугольник называется вписанным в окружность, если он касается ее всеми вершинами (рис.17a ).

Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника (рис.18).

Синус острого угла x противолежащего катета к гипотенузе.
Обозначается так: sin x .

Косинус острого угла x прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.
Обозначается так: cos x .

Тангенс острого угла x - это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg x .

Котангенс острого угла x - это отношение прилежащего катета к противолежащему.
Обозначается так: ctg x .

Правила:

Катет, противолежащий углу x , равен произведению гипотенузы на sin x :

b = c · sin x

Катет, прилежащий к углу x , равен произведению гипотенузы на cos x :

a = c · cos x

Катет, противоположный углу x , равен произведению второго катета на tg x :

b = a · tg x

Катет, прилежащий к углу x , равен произведению второго катета на ctg x :

a = b · ctg x .

Для любого острого угла x :

sin (90° - x ) = cos x

cos (90° - x ) = sin x

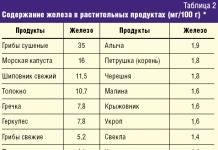
При решении различного рода задач, как сугубо математического, так и прикладного характера (особенно в строительстве), нередко требуется определить значение высоты определенной геометрической фигуры. Как рассчитать данную величину (высоту) в треугольнике?

Если мы попарно совместим 3 точки, расположенные не на единой прямой, то полученная фигура будет треугольником. Высота – часть прямой из любой вершины фигуры, которая при пересечении с противоположной стороной образует угол 90°.

Найти высоту в разностороннем треугольнике

Определим значение высоты треугольника в случае, когда фигура имеет произвольные углы и стороны.

Формула Герона

h(a)=(2√(p(p-a)*(p-b)*(p-c)))/a, где

p – половина периметра фигуры, h(a) – отрезок к стороне a, проведенный под прямым углом к ней,

p=(a+b+c)/2 – расчет полупериметра.

В случае наличия площади фигуры для определения ее высоты можно воспользоваться соотношением h(a)=2S/a.

Тригонометрические функции

Для определения длины отрезка, который составляет при пересечении со стороной a прямой угол, можно воспользоваться следующими соотношениями: если известна сторона b и угол γ или сторона c и угол β, то h(a)=b*sinγ или h(a)=c*sinβ.
Где:
γ – угол между стороной b и a,
β – угол между стороной c и a.

Взаимосвязь с радиусом

Если исходный треугольник вписан в окружность, для определения величины высоты можно воспользоваться радиусом такой окружности. Центр ее расположен в точке, где пересекаются все 3 высоты (из каждой вершины) – ортоцентре, а расстояние от него и до вершины (любой) – радиус.

Тогда h(a)=bc/2R, где:
b, c – 2 другие стороны треугольника,
R – радиус описывающей треугольник окружности.

Найти высоту в прямоугольном треугольнике

В данном виде геометрической фигуры 2 стороны при пересечении образуют прямой угол – 90°. Следовательно, если требуется определить в нем значение высоты, то необходимо вычислить либо размер одного из катетов, либо величину отрезка, образующего с гипотенузой 90°. При обозначении:
a, b – катеты,
c – гипотенуза,
h(c) – перпендикуляр на гипотенузу.
Произвести необходимые расчеты можно с помощью следующих соотношений:

• Пифагорова теорема:

a=√(c 2 -b 2),
b=√(c 2 -a 2),
h(c)=2S/c,т.к. S=ab/2,то h(c)=ab/c .

• Тригонометрические функции:

a= c*sinβ,
b=c* cosβ,
h(c)=ab/c=с* sinβ* cosβ.

Найти высоту в равнобедренном треугольнике

Данная геометрическая фигура отличается наличием двух сторон равной величины и третьей – основанием. Для определения высоты, проведенной к третьей, отличной стороне, на помощь приходит теорема Пифагора. При обозначениях
a – боковая сторона,
c – основание,
h(c) – отрезок к c под углом 90°, то h(c)=1/2 √(4a 2 -c 2).

Урок содержит описание свойств и формулы нахождения высоты треугольника, а также примеры решения задач. Если Вы не нашли решение подходящей задачи - пишите про это на форуме . Наверняка, курс будет дополнен.

ВЫСОТА ТРЕУГОЛЬНИКА Высота треугольника – опущенный из вершины треугольника перпендикуляр, проведенный на противолежащую вершине сторону или на ее продолжение. Свойства высоты треугольника: Если в треугольнике две высоты равны, то такой треугольник - равнобедренный В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащих на двух сторонах, непараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины этой стороны всегда можно провести окружность В остроугольном треугольнике две его высоты отсекают от него подобные треугольники Минимальная высота в треугольнике всегда проходит внутри этого треугольника Ортоцентр треугольника Все три высоты треугольника (проведенные из трех вершин) пересекаются в одной точке, которая называется ортоцентром . Для того, чтобы найти точку пересечения высот, достаточно провести две высоты (две прямые пересекаются только в одной точке). Расположение ортоцентра (точка О) определяется видом треугольника. У остроугольного треугольника точка пересечения высот находится в плоскости треугольника. (Рис.1). У прямоугольного треугольника точка пересечения высот совпадает с вершиной прямого угла (Рис.2). У тупоугольного треугольника точка пересечения высот находится за плоскостью треугольника (Рис.3). У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают. У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

ВИСОТА ТРИКУТНИКА Висота трикутника - опущений з вершини трикутника перпендикуляр, проведений на протилежну вершині бік або на її продовження. Всі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром. Для того, щоб знайти точку перетину висот, досить провести дві висоти (дві прямі перетинаються тільки в одній точці). Розміщення ортоцентра (точка О) визначається видом трикутника. У гострокутного трикутника точка перетину висот знаходиться в площині трикутника. (Мал.1). У прямокутного трикутника точка перетину висот збігається з вершиною прямого кута (Мал.2). У тупоугольного трикутника точка перетину висот знаходиться за площиною трикутника (Мал.3). У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються. У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються.

Формулы нахождения высоты треугольника

Рисунок приведен для облегчения восприятия формул нахождения высоты треугольника. Общее правило - длина стороны обозначена маленькой буквой, лежащей напротив соответствующего угла. То есть сторона a лежит напротив угла A.
Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена.

Другие обозначения:
a,b,c - длины сторон треугольника
h a - высота треугольника, проведенная к стороне a из противолежащего угла
h b - высота, проведенная к стороне b
h c - высота, проведенная к стороне c
R - радиус описанной окружности
r - радиус вписанной окружности

Пояснения к формулам.
Высота треугольника равна произведению длины стороны, прилежащей к углу, из которой опущена эта высота на синус угла между этой стороной и стороной, на которую такая высота опущена (Формула 1)
Высота треугольника равна частному от деления удвоенной величины площади треугольника на длину стороны, к которой опущена эта высота (Формула 2)
Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).
Высоты сторон в треугольнике соотносятся между собой в той же самой пропорции, как соотносятся между собой обратные пропорции длин сторон этого же треугольника, а также в той же самой пропорции между собой относятся произведения пар сторон треугольника, которые имеют общий угол (Формула 5).
Сумма обратных значений высот треугольника равна обратному значению радиуса вписанной в такой треугольник окружности (Формула 6)
Площадь треугольника можно найти через длины высот этого треугольника (Формула 7)
Длину стороны треугольника, на которую опущена высота, можно найти через применение формул 7 и 2.

Задача на .

В прямоугольном треугольнике ABC (угол C = 90 0) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см

Решение .

Треугольники ABC, ACD и CBD подобны между собой. Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).

Прямоугольные треугольники - единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.

Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)

Треугольники ABC и CBD подобны. Значит:

AD/DC = DC/BD, то есть

Задача на применение теоремы Пифагора.

Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см. Разность отрезков BD-AD=5 см.

Найти: Стороны треугольника ABC.

Решение .

1.Составим систему уравнений согласно теореме Пифагора

CD 2 +BD 2 =BC 2

CD 2 +AD 2 =AC 2

поскольку CD=6

Поскольку BD-AD=5, то

BD = AD+5, тогда система уравнений принимает вид

36+(AD+5) 2 =BC 2

Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой - равенство не будет нарушено. Получим:

36+36+(AD+5) 2 +AD 2 =AC 2 +BC 2

72+(AD+5) 2 +AD 2 =AC 2 +BC 2

2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:

AC 2 +BC 2 =AB 2

Поскольку AB=BD+AD, уравнение примет вид:

AC 2 +BC 2 =(AD+BD) 2

Поскольку BD-AD=5, то BD = AD+5, тогда

AC 2 +BC 2 =(AD+AD+5) 2

3. Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:

72+(AD+5) 2 +AD 2 =AC 2 +BC 2

AC 2 +BC 2 =(AD+AD+5) 2

Они имеют общую часть AC 2 +BC 2 . Таким образом, приравняем их друг к другу.

72+(AD+5) 2 +AD 2 =(AD+AD+5) 2

72+AD 2 +10AD+25+AD 2 =4AD 2 +20AD+25

2AD 2 -10AD+72=0

В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:

Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.

Соответственно

AB = BD + AD = 4 + 9 = 13

По теореме Пифагора находим остальные стороны треугольника:

AC = корень из (52)